Bereiche komplett auf- oder zuklappen:


2 Prozessbezogene Bereiche, inhaltsbezogene Bereiche und verbindliche Kontexte
Die in Kapitel 1 beschriebene übergreifende fachliche Kompetenz wird ausdifferenziert, indem prozessbezogene Bereiche und inhaltsbezogene Bereiche ausgewiesen werden. Dieses analytische Vorgehen erfolgt, um die Strukturierung der fachlichen Prozesse einerseits sowie der fachlichen Gegenstände andererseits transparent zu machen. In konkreten Lern- und Anforderungssituationen werden beide Seiten miteinander verknüpft.
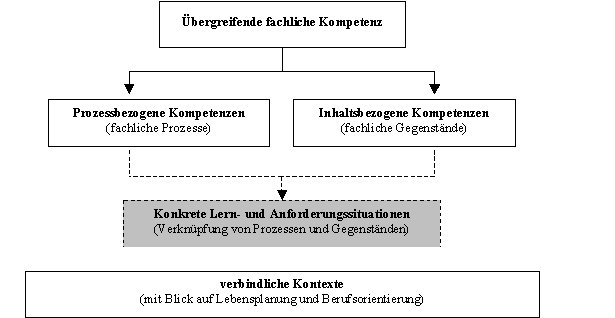
Prozessbezogene Bereiche repräsentieren die Grunddimensionen des fachlichen Handelns. Sie dienen dazu, die einzelnen Teiloperationen entlang der fachlichen Kerne zu strukturieren und für die am Lehr-Lernprozess Beteiligten zu verdeutlichen.
Inhaltsbezogene Bereiche systematisieren mit ihren jeweiligen Schwerpunkten die im Unterricht der Hauptschule unverzichtbaren fachlichen Gegenstände und sind die verbindliche Grundlage für die inhaltliche Ausrichtung des Lehrens und Lernens.
Konkrete Lern- und Anforderungssituationen verknüpfen fachliche Prozesse und fachliche Gegenstände. Sie werden von den Lehrerinnen und Lehrern vor Ort im Rahmen der Absprachen der Fachkonferenz gestaltet.
Verbindliche Kontexte gewährleisten den Beitrag des Mathematikunterrichts der Hauptschule zur Lebensplanung und zur Berufsorientierung.
2.1 Prozessbezogene Bereiche und inhaltsbezogene Bereiche
Der Mathematikunterricht an der Hauptschule soll bei den Schülerinnen und Schülern die für den Hauptschulabschluss nach Klasse 10 bzw. für den Mittleren Schulabschluss verbindlichen mathematischen Kompetenzen in dem Umfang und der Höhe aufbauen, wie sie in den Bildungsstandards der KMK vorgesehen sind. Mit der Zielperspektive eines allgemeinbildenden Mathematikunterrichts lassen sich durch eine Analyse der Geschichte und Struktur der Disziplin und der Befunde zum Lehren und Lernen von Mathematik zentrale prozessbezogene Bereiche und zentrale inhaltsbezogene Bereiche identifizieren, die das curriculare Grundgerüst des Faches darstellen:
|
Prozessbezogene Bereiche (fachliche Prozesse) |
Inhaltsbezogene Bereiche (fachliche Gegenstände) | ||
|---|---|---|---|
 |
Modellieren |  |
Arithmetik/Algebra |
 |
Problemlösen |  |
Geometrie |
 |
Argumentieren |  |
Funktionen |
 |
Kommunizieren |  |
Stochastik |
 |
Werkzeuge nutzen | ||
Die prozessbezogenen Bereiche spiegeln die für das Fach charakteristischen und die für fachliches Arbeiten notwendigen Prozesse wider. Für das Entstehen und Betreiben von Mathematik sind die folgenden drei Prozesse zentral und charakteristisch:
- Modellieren: Mathematik ist aus konkreten Fragestellungen des Alltags entstanden. Das Modellieren ist der Prozess der Beschreibung außermathematischer Realität durch mathematische Begriffe und Zusammenhänge sowie die Nutzung mathematischer Zusammenhänge zur Lösung realer Probleme.
- Problemlösen: Die mathematische Bearbeitung außer- oder innermathematischer Kontexte führt immer wieder zu Problemstellungen, die (zunächst) nicht schematisch oder in direkter Anlehnung an bekannte Muster bearbeitet werden können. Das Problemlösen ist der Prozess der Beantwortung solcher Problemstellungen durch Erkundung, Anwendung heuristischer Strategien und Reflexion von Lösungsansätzen.
- Argumentieren: Bei der Auseinandersetzung mit mathematischen Begriffen und mathematischen Zusammenhängen werden immer wieder neue Zusammenhänge entdeckt oder vermutet. Das Argumentieren ist der Prozess des Begründens und Beweisens mathematischer Zusammenhänge durch Rückgriff auf Bekanntes und die Regeln des mathematischen Schlussfolgerns.
Beim mathematischen Arbeiten treten neben die charakteristischen Prozesse noch die folgenden unterstützenden fachspezifischen Prozesse, ohne die mathematisches Arbeiten nicht denkbar ist:
- Kommunizieren:Die individuelle mathematische Bearbeitung von Fragestellungen benötigt Möglichkeiten der verbalen und nicht-verbalen Darstellung von mathematischen Begriffen und Zusammenhängen. Im sozialen Austausch müssen diese Darstellungen intersubjektiv nachvollziehbar sein und bestehende Konventionen berücksichtigen. Das Kommunizieren ist der Prozess der Dokumentation fachlicher Bearbeitungen und des Austausches über fachliche Bearbeitungen. Für die Mathematik sind neben der verbalen Darstellung insbesondere die ikonische und die symbolische Darstellung von zentraler Bedeutung.
- Werkzeuge nutzen:Bei der mathematischen Bearbeitung komplexerer Fragestellungen treten immer wieder gleiche Routinen auf, deren Erledigung von digitalen und nicht-digitalen Werkzeugen zuverlässig und wiederholbar übernommen werden kann. Das Nutzen von Werkzeugen ist der Prozess des Delegierens solcher fachlicher Routinen an geeignete Werkzeuge, sodass die Bearbeitung einer Fragestellung auf den eigentlichen mathematischen Kern konzentriert werden kann.
Die inhaltsbezogenen Bereiche strukturieren die fachlichen Gegenstände und die direkt auf sie bezogenen kognitiven Prozesse, die für einen allgemeinbildenden Mathematikunterricht in der Sekundarstufe I relevant sind:
- Arithmetik/Algebra – mit Zahlen und Symbolen umgehen können: Die Absicht, Anzahlen zu erfassen und mit ihnen umzugehen, hat zur Entwicklung des Zahlbegriffs und von Rechenoperationen geführt. Die Arithmetik umfasst diesen konkreten Umgang mit Zahlen, der uns im Alltag vor allem im Sachrechnen begegnet. Die Verallgemeinerung des konkreten Umgangs mit Zahlen durch symbolische Elemente (Variablen) und die Erweiterung der Zahlbereiche (von den natürlichen Zahlen bis hin zu reellen Zahlen) sind Gegenstand der Algebra.
- Geometrie – ebene und räumliche Strukturen nach Maß und Form erfassen können: Fragestellungen aus der Landvermessung, die vor allem die Bestimmung von Längen und Flächeninhalten betrafen, haben zu einer systematischen Beschäftigung mit Figuren in der Ebene und im Raum geführt. Die Geometrie umfasst den quantitativen und den qualitativen Umgang mit ebenen und räumlichen Strukturen.
- Funktionen – Beziehungen und Veränderungen erkunden und beschreiben können: Die moderne Mathematik ist vor allem durch die simultane Betrachtung zweier Größen geprägt, wobei eine als von der anderen abhängig betrachtet wird. Funktionen sind mathematische Modelle für solche Zusammenhänge. Funktionales Denken ist grundlegend für das Verstehen einer technologisierten und ökonomisierten Welt.
- Stochastik – mit Daten und Zufall arbeiten können: Der mathematische Umgang mit Daten erlaubt es, viele Fragestellungen des Alltags rational, quantitativ zu bearbeiten. Zufallserscheinungen wurden historisch zunächst separat hiervon betrachtet, bis die moderne mathematische Statistik erfasst hat, dass viele Daten zufallsbedingt entstehen. Die Stochastik umfasst die Mathematik der Daten und des Zufalls.
Im Sinne erwarteter mathematischer Kompetenz ist prinzipiell jede Verknüpfung von fachlichen Prozessen und fachlichen Gegenständen denkbar und relevant. Dennoch muss der Unterricht nicht jede einzelne Verknüpfung explizit in den Blick nehmen, da weder einzelne Gegenstände an bestimmte Prozesse noch einzelne Prozesse an bestimmte Gegenstände gebunden sind. Es liegt in der Verantwortung der Fachkonferenzen und der einzelnen Lehrerinnen und Lehrer fachliche Prozesse, fachliche Gegenstände und geeignete Kontexte in den schulinternen Lehrplänen und in konkreten Lern- und Anforderungssituationen so zu verknüpfen, dass den Schülerinnen und Schülern ein breiter Kompetenzerwerb ermöglicht wird und dass ein kohärentes Bild fachlichen Handelns entsteht:
„Mathematik können“ auf dem Niveau dieses Kernlehrplans bedeutet, dass die Schülerinnen und Schüler die in 2.1.1 beschriebenen Prozesse (vollständig) mit den in 2.1.2 enthaltenen fachlichen Gegenständen (ihrem curricularen Alter entsprechend) ausüben können.
2.1.1 Prozessbezogene Kompetenzen
In den fünf prozessbezogenen Bereichen werden die für das Fach charakteristischen Prozesse Modellieren, Problemlösen und Argumentieren sowie die unterstützenden Prozesse Kommunizieren und Werkzeuge nutzen mit verbindlichen Kompetenzerwartungen dargestellt.
Eine Progression hinsichtlich der mit den Prozessen verbundenen Anforderungshöhe resultiert kaum aus den Prozessen selbst. Vielmehr können Schülerinnen und Schüler die Prozesse schon zu Beginn der Sekundarstufe I im Wesentlichen vollständig ausüben. Die beim fachlichen Handeln beobachtbaren Unterschiede zwischen jüngeren und älteren Schülerinnen und Schülern lassen sich – neben entwicklungspsychologischen Faktoren – überwiegend auf die Progression in den inhaltsbezogenen Bereichen zurückführen.
Die Progression in den inhaltsbezogenen Bereichen wird in Kap. 2.1.2 dargestellt. Entwicklungspsychologische Faktoren sind bezüglich der mathematischen Prozesse wirksam, da mit zunehmendem Alter der Schülerinnen und Schüler auch deren Abstraktionsfähigkeit und die Fähigkeit, eigene Lernprozesse zu reflektieren (Metakognition), zunimmt. Darüber hinaus werden die Situationen der Weltbegegnung vielfältiger und differenzierter, so dass mehr und komplexere Situationen zugänglich werden. Diese tendenziell mit dem Alter der Kinder und Jugendlichen wachsenden Möglichkeiten bedingen eine Progression bei den prozessbezogenen Kompetenzen bis zum Ende der Sekundarstufe I.
Eine abschlussbezogene Differenzierung mathematischer Kompetenz in der Doppeljahrgangsstufe 9/10 ergibt sich wiederum aus der entsprechenden Differenzierung in den inhaltsbezogenen Bereichen. Daher wird bei der Darstellung der prozessbezogenen Kompetenzen nicht nach Doppeljahrgangsstufen differenziert. Eine Differenzierung zwischen den beiden Abschlussniveaus ist nur im Bereich Werkzeuge nutzen ausgewiesen. Dies betrifft den Einsatz Dynamischer-Geometrie-Software, der eng mit der inhaltsbezogenen Differenzierung im Gebiet Geometrie verbunden ist.
|
Modellieren | |
|---|---|
|
Bereits ab Beginn der Jahrgangsstufe 5 wenden die Schülerinnen und Schüler Mathematik auf konkrete Fragestellungen aus ihrer Erfahrungswelt an. Dabei sollen sie mit den jeweils zur Verfügung stehenden fachlichen Gegenständen
Im weiteren Verlauf bis zum Ende der Jahrgangsstufe 10 sollen die Schülerinnen und Schüler zusätzlich
|
|
|
Problemlösen | |
|---|---|
|
Bereits ab Beginn der Jahrgangsstufe 5 bearbeiten die Schülerinnen und Schüler mathematische Fragestellungen, bei deren Lösung nicht unmittelbar auf erlernte Verfahren zurückgegriffen werden kann. Dabei sollen sie mit den jeweils zur Verfügung stehenden fachlichen Gegenständen
Im weiteren Verlauf bis zum Ende der Jahrgangsstufe 10 sollen die Schülerinnen und Schüler zusätzlich
|
|
|
Argumentieren | |
|---|---|
|
Bereits ab Beginn der Jahrgangsstufe 5 stellen die Schülerinnen und Schüler in zugänglichen mathematischen Situationen Vermutungen über Zusammenhänge auf und erarbeiten Begründungen. Dabei sollen sie mit den jeweils zur Verfügung stehenden fachlichen Gegenständen
Im weiteren Verlauf bis zum Ende der Jahrgangsstufe 10 sollen die Schülerinnen und Schüler zusätzlich
|
|
|
Kommunizieren | |
|---|---|
|
Bereits ab Beginn der Jahrgangsstufe 5 erfassen und verstehen die Schülerinnen und Schüler mathematikhaltige Darstellungen und stellen eigene Denkprozesse oder mathematische Situationen angemessen und nachvollziehbar dar. Dabei sollen sie mit den jeweils zur Verfügung stehenden fachlichen Gegenständen
Im weiteren Verlauf bis zum Ende der Jahrgangsstufe 10 sollen die Schülerinnen und Schüler zusätzlich (auch bei adressatenbezogenen Präsentationen)
|
|
|
Werkzeuge nutzen | |
|---|---|
|
Bereits ab Beginn der Jahrgangsstufe 5 nutzen die Schülerinnen und Schüler verschiedene (nicht-digitale) Werkzeuge für mathematisches Arbeiten. Beim Umgang mit den jeweils zur Verfügung stehenden fachlichen Gegenständen sollen sie die folgenden Werkzeuge nutzen können:
Im weiteren Verlauf bis zum Ende der Jahrgangsstufe 10 sollen die Schülerinnen und Schüler zusätzlich weitere (auch digitale) Werkzeuge nutzen können:
Dabei sollen sie die Eigenschaften dieser Werkzeuge darstellen, die Werkzeuge der jeweiligen Situation angemessen auswählen und Vor- und Nachteile des Einsatzes der Werkzeuge sowie möglicher Alternativen beurteilen können. zusätzlich Mittlerer Schulabschluss: |
|
2.1.2 Inhaltsbezogene Kompetenzen am Ende der Doppeljahrgangsstufen 5/6, 7/8 und 9/10
Die folgenden Kompetenzerwartungen beschreiben in den vier inhaltsbezogenen Bereichen einen verbindlichen Kern für den Mathematikunterricht an Hauptschulen. Es liegt in der Verantwortung der Fachkonferenzen und der einzelnen Lehrerinnen und Lehrer an geeigneten Stellen inhaltliche Vertiefungen oder Ergänzungen vorzunehmen. Dies soll vor allem mit Blick auf die mathematischen Prozesse geschehen.
Die Kompetenzerwartungen sind innerhalb der Bereiche für das Ende der Doppeljahrgangsstufen 5/6, 7/8 und 9/10 formuliert. Dabei werden für das Ende der Doppeljahrgangsstufen 7/8 und 9/10 Erwartungen benannt, die über den gemeinsamen Sockel hinaus für die E-Kurse bzw. für das Abschlussniveau Mittlerer Schulabschluss verbindlich sind.
Die für die Doppeljahrgangsstufen ausgewiesenen Kompetenzerwartungen berücksichtigen über die gesamte Sekundarstufe I hinweg für jeden Bereich den kumulativen Aufbau mathematischer Kompetenz nach dem Spiralprinzip. Dies bedeutet, dass einzelne inhaltliche Stränge, wie z. B. Berechnungen an ebenen Figuren oder der Umgang mit Daten, in jeder Doppeljahrgangsstufe präsent sind. Im Unterricht sollen fachliche Gegenstände in den höheren Jahrgangsstufen wieder aufgegriffen und vertieft betrachtet werden. Auch sollen in den unteren Jahrgangsstufen aus dem aktuellen fachlichen Gegenstand heraus propädeutisch Betrachtungen durchgeführt werden, die erst in späteren Jahrgangsstufen systematisiert werden. Dieser inhaltliche Aufbau ermöglicht eine intelligente Abfolge von Erarbeiten, Üben und Wiederholen.
Die folgenden inhaltsbezogenen Kompetenzerwartungen erfordern im Unterricht die Bearbeitung entsprechender fachlicher Gegenstände im Sinne der typischen mathematischen Prozesse (Modellieren, Problemlösen und Argumentieren) und der unterstützenden Prozesse (Kommunizieren und Werkzeuge nutzen) sowie die Vernetzung der vier inhaltsbezogenen Bereiche untereinander. Dies bedeutet insbesondere, dass alle fachlichen Gegenstände in ihrem potenziellen Beitrag zur Lösung alltäglicher außermathematischer Problemstellungen erfahrbar werden. Rechentechniken haben in diesem Zusammenhang eindeutig eine dienende Funktion und stellen keinen Selbstzweck dar.
|
Arithmetik/Algebra – mit Zahlen und Symbolen umgehen können | |
|---|---|
|
Ende 6 |
Die Schülerinnen und Schüler können
|
|
zusätzlich Ende 8 |
Die Schülerinnen und Schüler können
zusätzlich E-Kurs:
|
|
zusätzlich Ende 10 |
Die Schülerinnen und Schüler können
zusätzlich E-Kurs bzw. Mittlerer Schulabschluss:
|
|
Geometrie – ebene und räumliche Strukturen nach Maß und Form erfassen können | |
|---|---|
|
Ende 6 |
Die Schülerinnen und Schüler können
|
|
zusätzlich Ende 8 |
Die Schülerinnen und Schüler können
zusätzlich E-Kurs:
|
|
zusätzlich Ende 10 |
Die Schülerinnen und Schüler können
zusätzlich E-Kurs bzw. Mittlerer Schulabschluss:
|
|
Funktionen – Beziehungen und Veränderungen erkunden und beschreiben können | |
|---|---|
|
Ende 6 |
Die Schülerinnen und Schüler können
|
|
zusätzlich Ende 8 |
Die Schülerinnen und Schüler können
|
|
zusätzlich Ende 10 |
Die Schülerinnen und Schüler können
zusätzlich E-Kurs bzw. Mittlerer Schulabschluss:
|
|
Stochastik – mit Daten und Zufall arbeiten können | |
|---|---|
|
Ende 6 |
Die Schülerinnen und Schüler können
|
|
zusätzlich Ende 8 |
Die Schülerinnen und Schüler können
|
|
zusätzlich Ende 10 |
Die Schülerinnen und Schüler können
zusätzlich E-Kurs bzw. Mittlerer Schulabschluss:
|
2.2 Verbindliche Kontexte
Im Mathematikunterricht der Hauptschule sollen Begriffe, Zusammenhänge und Verfahren vor allem aus außermathematischen Kontexten heraus entwickelt werden bzw. in solchen Kontexten angewendet werden. Die konkrete Auswahl entsprechender Kontexte ist Aufgabe der Fachkonferenzen und der einzelnen Lehrerinnen und Lehrer.
Der Mathematikunterricht an der Hauptschule soll über die Entwicklung primär fachbezogener Kompetenzen hinaus wesentliche Beiträge für die Lebensplanung und die Berufsorientierung der Schülerinnen und Schüler leisten. Dies geschieht, indem die Schülerinnen und Schüler im Mathematikunterricht erfahren können,
- wie mathematische Kompetenzen bei der Lebensplanung – vor allem beim quantitativen Umgang mit Ressourcen (z. B. Geld, Zeit, Werkstoffe) – helfen können und
- welche mathematischen Kompetenzen in unterschiedlichen Berufsfeldern benötigt und angewendet werden.
Darüber hinaus kann der Mathematikunterricht dazu beitragen, dass Schülerinnen und Schüler sich –vorrangig mithilfe quantitativer, statistischer Daten (u. a. Arbeitsmarktdaten und Berufsprofile) – differenziert über verschiedene Berufe informieren.
Dieses Ziel kann vor allem durch die Auswahl geeigneter Kontexte für den Mathematikunterricht erreicht werden. Die folgende Übersicht enthält einige zentrale Kontexte für die Lebensplanung und die Berufsorientierung, die verbindlich für den Mathematikunterricht an der Hauptschule sind. Über diese wenigen verbindlichen Kontexte hinaus ist es Aufgabe der Fachkonferenzen und der einzelnen Lehrerinnen und Lehrer, weitere für die oben genannten Zielsetzungen relevante Kontexte mit Blick auf die Bedürfnisse der jeweiligen Lerngruppe und der einzelnen Schülerinnen und Schüler auszuwählen.
Die verbindlichen Kontexte werden in der Übersicht den Doppeljahrgangsstufen 5/6, 7/8 und 9/10 zugewiesen. Dabei wurde jeweils die thematische Nähe zu inhaltsbezogenen Kompetenzerwartungen (Kap. 2.1.2) berücksichtigt. Wenn mit Blick auf die langfristige Unterrichtsplanung vor Ort (z. B. im Sinne fächerverbindenden Unterrichts) eine Thematisierung in anderen Doppeljahrgangsstufen pädagogisch sinnvoll ist, darf entsprechend begründet von der Übersicht abgewichen werden. Dabei muss aber sichergestellt sein, dass alle verbindlichen Kontexte im Verlauf der Sekundarstufe I thematisiert werden.
|
Lebensplanung |
Berufsorientierung | |
|---|---|---|
|
5/6 |
|
|
|
7/8 |
|
|
|
9/10 |
|
|
|
Verbindliche Kontexte für den Mathematikunterricht in der Hauptschule |
||
Alle hier genannten verbindlichen Kontexte haben auch in anderen Fächern bzw. Lernbereichen eine besondere Relevanz. Die Thematisierung der verbindlichen Kontexte muss also fächerübergreifend erfolgen. So wird gewährleistet, dass für die Lebensplanung und die Berufsorientierung wichtige Kontexte nicht einseitig aus der Perspektive eines Fachs erscheinen.
2.3 Hinweise für einen sprachsensiblen Fachunterricht
Fachliches Lernen und sprachliches Lernen sind untrennbar miteinander verbunden. Sprache besitzt dabei eine besondere Bedeutung – zum einen für die fachliche Kommunikation, zum anderen aber auch für die fachlichen Verstehensprozesse und die begriffliche Erfassung von Welt. Das Denken in funktionalen Zusammenhängen etwa ist Schülerinnen und Schülern nur dann adäquat möglich, wenn sie über entsprechende sprachliche Mittel verfügen („Wie verändert sich …, wenn sich … verändert / immer größer wird / immer kleiner wird?“).
Sprachkompetenzentwicklung in Mathematik beschränkt sich somit keineswegs auf den Kompetenzbereich Kommunikation, sondern bestimmt alle Lernprozesse wesentlich mit. Bei der Auseinandersetzung mit fachtypischen Phänomenen müssen die jeweils förderlichen sprachlichen Mittel berücksichtigt werden. Dabei spielen die folgenden Sprachhandlungen eine zentrale Rolle. In der abschließenden Tabelle sind auf der Wortebene, der Satzebene und der Textebene einige Konventionen des fachlichen Sprachgebrauchs exemplarisch zusammengestellt.
Benennen, Definieren, Beschreiben
- Erfassen und präzises Bezeichnen fachlich relevanter Aspekte und Unterrichtsgegenstände (z. B. Objekte, Prozesse, Ereignisse, Themen und Problemstellungen der realen Welt und zugehöriger mathematischer Idealisierungen) anhand von fachbezogenen Begriffen
Berichten
- angemessene Wiedergabe mithilfe sachlicher Wortwahl (Vermeidung subjektiver Eindrücke) auch unter Verwendung von Fachsprache
- Nutzung des richtigen Tempusgebrauchs bei der Wiedergabe von vergangenen bzw. gültigen Ereignissen, Erlebnissen und Vorgängen
- Abstimmung des Informationsgehalts sowie der Abfolge von Informationen auf den konkreten Zweck des Berichts
Erklären, Erläutern
- angemessene Verbalisierung von Zusammenhängen, z. B. Beachtung logischer Verknüpfungen, adäquater Nebensatzkonstruktionen, Herstellung zeitlicher Bezüge
- Generalisierung von Zusammenhängen unter Beachtung vergangener und zukünftiger Prozesse und Ereignisse durch Präsensgebrauch und bestimmte Formulierungen, die vom Konkreten abweichen, z. B. im Allgemeinen, dann gilt, daraus folgt
- sachliche Äußerung unter Verwendung eines nicht emotionalen Sprachstils
Bewerten, Beurteilen
- überzeugendes Vertreten der eigenen Position durch klare adressatenbezogene Sprache
- Beurteilung und Bewertung z. B. von Sachverhalten, Ereignissen und Verhaltensweisen unter Verwendung begründender Formulierungen
Argumentieren, Stellung beziehen
- Unterscheidung zwischen faktengestützten Aussagen und Annahmen durch Erkennen bzw. eigene Verwendung sprachlicher Signale, die die Validität untermauern, abschwächen oder widerlegen, z. B. wahrscheinlich, bestimmt, vermutlich, eventuell
- Untermauern der eigenen Position durch Formulierung von Begründungen, Abwägung, Verknüpfung, z. B. zwar, jedoch, aber, dennoch, durchaus
Im Einzelnen bedeutet dies:
Wortebene
- Unterscheidung zwischen Umgangs- und Standardsprache, z. B. keiner, was, egal / niemand, etwas, gleichgültig
- Möglichkeiten der präziseren Begrifflichkeit, Nuancierung und Differenzierung des standardsprachlichen Wortschatzes durch Adjektive, durch Adverbien, durch adverbiale Ergänzungen, z. B. Adjektive: typisch, heftig, gut; Adverbien: dorthin, vermutlich, bergauf; adverbiale Ergänzungen: Wissenschaftler sollten unabhängig von persönlichen Vorlieben Sachverhalte objektiv darstellen., Die Vermutung wird durch unsere Messungen im vollen Umfang bestätigt., Ich habe mehrere Male versucht, ein geeignetes Mischungsverhältnis zu bestimmen.
- sachbezogener und fachsprachlicher Wortschatz
- Bedeutungsänderung in fachsprachlichen Kontexten, z. B. schneiden, Operation, Funktion, faires Spiel, Folge, Potenz
- Bedeutungen von Formeln, Symbolen, Maßeinheiten, Ziffern, Sonderzeichen (z. B. m (Masse), m (Meter), kg, f(x), +, >)
Nominalisierungen verdichten, z. B. Durch Verdopplung des Ergebnisses erhält man eine ganze Zahl. = Wenn man das Ergebnis verdoppelt, erhält man eine ganze Zahl.
Satzebene
- komplexere Satzkonstruktionen, um Zusammenhänge und Beziehungen darzustellen: zeitlich, z. B. danach; begründend, z. B. wenn… dann; bedingend, z. B. unter der Voraussetzung, dass…)
- funktionsgerechte sprachliche Signale, z. B. Signale der Thesenformulierung, der Gegenüberstellung, des Belegens, des Abwägens, der Schlussfolgerung, der alternativen Möglichkeiten
- fachliche Konventionen:
- Tempusgebrauch, z. B. Präsens bei der Beschreibung von Algorithmen
- Konjunktivgebrauch, z. B. Annahmen, Gedankenexperimente, Variation von Größen
- Sachverhalte zur Generalisierung entpersonalisieren durch Passiv oder durch unpersönliches Subjekt, z. B. bei der Beschreibung von Regeln und Verfahren („Man kann den Flächeninhalt eines Rechtecks berechnen, indem man die beiden Seitenlängen multipliziert.“)
Textebene
- globale Kohärenz: inhaltlicher Gesamtzusammenhang, „roter Faden“ eines Textes: z. B. schlüssige, bruchlose Darstellung von Zusammenhängen, Berücksichtigung inhaltlicher und sprachlicher Zusammenhänge, die rückverweisende bzw. eindeutige Verwendung eines Pronomens auf den vorherigen Absatz
- Adressat: z. B. Sprachstil den Zuhörern anpassen; zielorientiert: z. B. werbend, informierend-situationsorientiert: z. B. Informationsstand bekannt/unbekannt à ggf. vorheriges Erklären von Fachbegriffen
- Berücksichtigung fachspezifischer Textsorten; z. B. Beschreibung von Algorithmen, Definition, Bericht, Artikel, Sachbuch
- Unterscheidung zwischen Schriftsprache und gesprochener Sprache (schriftlich (s): keine unmittelbare Situations- und Handlungseinbindung / mündlich (m): Situations- und Handlungseinbindung):
- (s): Wahrnehmungsraum von Sender und Empfänger nicht identisch: im Anschluss daran, hinter dem Schnittpunkt, auf der gegenüberliegenden Seite / (m): gemeinsamer Wahrnehmungsraum, auf den man verweisen kann: dann, dort, da drüben
- (s): Planungszeit / (m): Flüchtigkeit
- (s): keine weiteren Informationsträger / (m): weitere Informationsträger: Gestik, Mimik, Tonfall
- (s): Exaktheit der Begriffe: niemand, etwas, gleichgültig / (m): Toleranz in der Begrifflichkeit: keiner, was, egal


 Kontakt
Kontakt