2  Bereiche und Schwerpunkte

Grundlegende mathematische Bildung zeigt sich in fachbezogenen Kompetenzen, d. h. durch das Zusammenspiel von Kompetenzen, die sich primär auf Prozesse beziehen (prozessbezogene Kompetenzen), und solchen, die sich primär auf Inhalte beziehen (inhaltsbezogene Kompetenzen). Sie entwickeln sich bei der aktiven Auseinandersetzung der Schülerinnen und Schüler mit mathematischen Situationen.
Prozessbezogene Kompetenzen werden in der aktiven Auseinandersetzung mit konkreten Lerninhalten, also unter Nutzung inhaltsbezogener Kompetenzen, erworben und weiterentwickelt. Zugleich unterstützen prozessbezogene Kompetenzen den verständigen Erwerb inhaltsbezogener Fertigkeiten und Fähigkeiten. Die prozessbezogenen und die inhaltsbezogenen Kompetenzen sind auf vielfältige Art miteinander verwoben.

Dem Erkennen und Nutzen von Mustern und Strukturen kommt eine wesentliche Rolle im Mathematikunterricht zu. Muster und Strukturen bestimmen häufig die einzelnen Themenbereiche und können zur Verdeutlichung zentraler mathematischer Grundideen genutzt werden. Von daher werden sie im Folgenden nicht als eigener Bereich ausgewiesen, sondern sind integraler Bestandteil aller Bereiche.

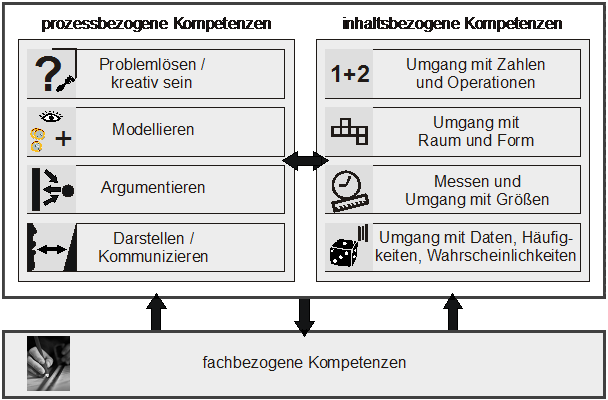
Die acht Bereiche des Faches Mathematik in der Grundschule werden im Folgenden kurz umrissen. In Kapitel 3 werden sie durch Kompetenzerwartungen zum Ende der Schuleingangsphase bzw. zum Ende der Klasse 4 konkretisiert.

Die Bereiche und die ihnen zugeordneten Schwerpunkte sind verbindlich. Unterrichtsthemen und -reihen sind so zu gestalten, dass die Schülerinnen und Schüler die ausgewiesenen Kompetenzerwartungen nachhaltig erreichen. Bei der Planung und Durchführung des Unterrichts wirken die Bereiche für die Gestaltung komplexer Lernsituationen integrativ zusammen.

 

2.1 Prozessbezogene Bereiche

Prozessbezogene Kompetenzen zeigen sich in der lebendigen Auseinandersetzung mit Mathematik. Auf die gleiche Weise werden sie in der tätigen Auseinandersetzung erworben. Die angestrebten Formen der Nutzung von Mathematik müssen daher auch regelmäßig genutzte Formen des Mathematiklernens sein. Von zentraler Bedeutung für eine erfolgreiche Nutzung und Aneignung von Mathematik sind vor allem die folgenden vier prozessbezogenen Kompetenzen.

Problemlösen/kreativ sein
Die Schülerinnen und Schüler bearbeiten Problemstellungen. Dabei erschließen sie Zusammenhänge, stellen Vermutungen an, probieren systematisch, reflektieren und prüfen, übertragen, variieren und erfinden.

Modellieren
Die Schülerinnen und Schüler wenden Mathematik auf konkrete Aufgabenstellungen aus ihrer Erfahrungswelt an. Dabei erfassen sie Sachsituationen, übertragen sie in ein mathematisches Modell und bearbeiten sie mithilfe mathematischer Kenntnisse und Fertigkeiten. Ihre Lösung beziehen sie anschließend wieder auf die Sachsituation.

Argumentieren
Die Schülerinnen und Schüler stellen begründet Vermutungen über mathematische Zusammenhänge unterschiedlicher Komplexität an und erklären Beziehungen und Gesetzmäßigkeiten (sprachlich, handelnd, zeichnerisch).

Darstellen/Kommunizieren
Die Schülerinnen und Schüler stellen eigene Denkprozesse oder Vorgehensweisen angemessen und nachvollziehbar dar und tauschen sich darüber mit anderen aus. Dies kann sowohl verbal in mündlicher oder schriftlicher Form als auch durch den Einsatz von anderen Darstellungsformen wie Skizzen, Tabellen usw. geschehen. Sie kommunizieren im Unterricht über mathematische Gegenstände und Beziehungen in der Umgangssprache und zunehmend auch in der fachgebundenen Sprache mit fachspezifischen Begriffen.

 

2.2 Inhaltsbezogene Bereiche

Die inhaltsbezogenen Kompetenzen orientieren sich an mathematischen Leitideen, die für den gesamten Mathematikunterricht – für die Grundschule und für das weiterführende Lernen – von fundamentaler Bedeutung sind.

Zahlen und Operationen

Auf der Grundlage tragfähiger Zahl- und Operationsvorstellungen sowie verlässlicher Kenntnisse und Fertigkeiten entwickeln und nutzen die Schülerinnen und Schüler Rechenstrategien, rechnen überschlagend und führen die schriftlichen Rechenverfahren verständig aus.

Schwerpunkte sind:

• Zahlvorstellungen
• Operationsvorstellungen
• Schnelles Kopfrechnen
• Zahlenrechnen
• Ziffernrechnen
• Überschlagendes Rechnen
• Flexibles Rechnen.

Raum und Form

Die Schülerinnen und Schüler schulen ihre Raumorientierung und ihre Raumvorstellung und sammeln durch handelnden Umgang Grunderfahrungen zu Eigenschaften und Maßen von ebenen Figuren und Körpern (z. B. Umfang und Flächeninhalt), zu den Auswirkungen geometrischer Operationen und zu geometrischen Eigenschaften wie Symmetrie. Sie entwickeln gezielt ihre zeichnerischen Fertigkeiten.

Schwerpunkte sind:

• Raumorientierung und Raumvorstellung
• Ebene Figuren
• Körper
• Symmetrie
• Zeichnen.

Größen und Messen

Die Schülerinnen und Schüler entwickeln und nutzen tragfähige Größenvorstellungen ebenso wie einen Grundbestand an Kenntnissen und Fertigkeiten beim Umgang mit Größen und bei der Bearbeitung von Sachproblemen aus der Lebenswirklichkeit.

Schwerpunkte sind:

• Größenvorstellungen und Umgang mit Größen
• Sachsituationen.

Daten, Häufigkeiten und Wahrscheinlichkeiten

Die Schülerinnen und Schüler erheben Daten und stellen sie unterschiedlich dar. Sie bewerten sie in Bezug auf konkrete Fragestellungen und schätzen die Wahrscheinlichkeit einfacher Ereignisse ein.

Schwerpunkte sind:

• Daten und Häufigkeiten
• Wahrscheinlichkeiten.