Die Auswahl von Aufgaben für den Unterricht im Hinblick auf Niveaudifferenzierung und Aufgabenvariation
Aufgabenvariation
Zur individuellen Förderung sind Lernaufgaben erforderlich, die universell zugänglich sind. Solche Aufgaben werden so flexibel gestaltet, dass sie von den Lernenden individuell auf unterschiedlichen Lernniveaus bearbeitet werden können und allen Lernenden individuell angepasste Lernfortschritte und Könnenserfahrungen ermöglichen. Die nachfolgende Übersicht zeigt drei Postulate der universellen Zugänglichkeit und drei sich daraus ergebende Prinzipien der Unterrichtsgestaltung.
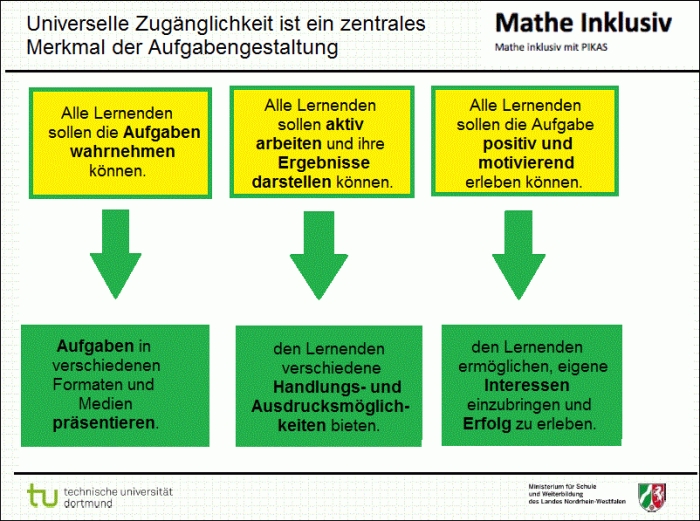
Die Adaption von Lernaufgaben erfolgt unter acht Leitideen. Diese sind nachfolgend dargestellt und durch Beispiele aus dem Unterricht illustriert.
Unterschiedliche Darstellungsformen nutzen
Aufgaben lassen sich auf drei Repräsentationsebenen darstellen. Die enaktive Ebene ermöglicht einen handelnden Zugang zu den Lerngegenständen. Dabei ist der Einsatz von realen Alltagsgegenständen wesentlich, um Lernaufgaben anschaulich zu illustrieren (Bsp.: Rechenoperationen mit Alltagsgegenständen, zum Beispiel mit Bonbons). Die ikonische Ebene ermöglicht einen bildlichen Zugang zu den Lerngegenständen. Der Einsatz von Bildmaterial ist für die Basis-Lernaufgaben anschaulich zu illustrieren (Bsp.: Rechenoperation Subtraktion: auf einem Bild fliegt etwas weg, fällt etwas um oder wird etwas weggenommen). Die symbolische Ebene sieht einen abstrakten Zugang zu den Lerngegenständen vor. Mathematische Lernaufgaben werden hier durch Kombinationen von Ziffern und Symbolen dargestellt. Natürlich ist es immer möglich, die drei Repräsentationsebenen miteinander zu kombinieren. Dies verdeutlicht das Schaubild.
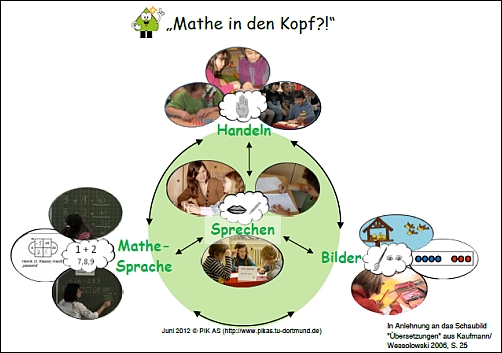
Grafik Repräsentationsebenen, Quelle: Pik As (PDF, 2,1 MB)
Verschiedene Vorgehensweisen ermöglichen
Die Aufgabe 27 + 15 kann z.B. auf zwei verschiedenen Wegen gelöst werden.
Mit der Strategie „Zehner extra, Einer extra“ werden beide Summanden in die Stellenwerte zerlegt. Gerechnet wird zunächst 20 + 10 = 30 und dann 7 + 5 = 15. Die Teilergebnisse werden dann addiert. Die Notation erfolgt stellengerecht untereinander.
Möglich ist aber auch die Strategie „Schrittweise rechnen“. Dabei wird ein Summand in die Stellenwerte zerlegt. Gerechnet wird zunächst 27 + 10 = 37 und dann 37 + 5 = 42. Die Notation erfolgt stellengerecht untereinander.
In Rechenkonferenzen können diese verschiedenen Strategien mit den Kindern besprochen werden. Die letztendliche Wahl liegt beim Kind. Quelle: Pik As (PDF, 1050KB)
Forschermittel nutzen
Die Nutzung von Darstellungs- und Veranschaulichungsmitteln ist in der Schule häufig negativ besetzt, da mit ihr das Vorliegen einer Lernschwäche assoziiert wird (Bsp.: Nutze Plättchen als Hilfe.). Der Begriff „Forschermittel“ führt zu einer positiven Assoziation, da mit ihr die Entdeckerfreude suggeriert wird. Eine Übersicht zu verschiedenen Forschermitteln kann auch als Plakat in der Klasse aufgehängt werden.
Den gemeinsamen Austausch vorbereiten
Der Austausch über Rechen- und Denkwege kann z.B. in einer Mathekonferenz unter verschiedenen Kindern stattfinden, optional mit Beteiligung der Lehrkraft. Die Erklärung des eigenen Rechenwegs für andere hilft, ein gesicherteres Verständnis für mathematische Problemsituationen zu entwickeln. Der gemeinsame Austausch kann beispielsweise in einer Rechenkonferenz erfolgen. Einen möglichen Ablauf einer Mathekonferenz finden sie hier (PDF, 92,4KB).
Die Anforderungsbereiche berücksichtigen
Die Bildungsstandards beschreiben 3 Niveaustufen (Anforderungsbereiche I – III) von Aufgaben:
- AB I: Reproduzieren: Das Lösen der Aufgabe erfordert Grundwissen und das Ausführen von Routinetätigkeiten
- AB II: Zusammenhänge herstellen: Das Lösen der Aufgabe erfordert das Erkennen und Nutzen von Zusammenhängen
- AB III: Verallgemeinern und Reflektieren: Das Lösen der Aufgabe erfordert komplexe Tätigkeiten wie Strukturieren, Entwickeln von Strategien, Beurteilen und Verallgemeinern. (Quelle: PIK AS (PDF, 80,7KB), S.2f)
„Die Anforderungsbereiche sind in ihrem Abstraktionsgrad ansteigend. Es wird deutlich, dass die Bearbeitung von Aufgabenstellungen auf AB II und AB III prozessbezogene Kompetenzen erfordert. (...) Bei der Einschätzung des Schwierigkeitsgrades einer Aufgabe ist allerdings zu berücksichtigen, dass diese nicht immer eindeutig vorzunehmen ist. So hängen die tatsächlichen Anforderungen z.B. auch von den Vorerfahrungen, vom Grad der Vertrautheit einer Aufgabenstellung und vor allem auch von den bereits praktizierten Formen des Lernens ab. Auch können Aufgaben auf sehr unterschiedlichen Niveaustufen gelöst werden, vom unsystematischen Ausprobieren bis hin zu abstrakt-strategischen, vorausschauenden Überlegungen." (Quelle: PIK AS (PDF, 80,7KB), S. 3)
Beispiele für Aufgaben zu den drei Anforderungsbereichen, Quelle: PIK AS (PDF, 80,7KB)
Verwandte Aufgabenstellungen verwenden
Die Schülerinnen und Schülern wählen in der Regel zwischen zwei oder mehreren Aufgaben mit gleicher oder ähnlicher Struktur, aber unterschiedlichen Inhalten. Diese zeichnen sich durch analoge Aufgabenanforderungen aus, die sich in Anspruch und Komplexität unterscheiden und im Sinne des Spiralprinzips aufeinander aufbauen.
Das nachfolgende Beispiel zeigt zwei Aufgaben der gleichen Struktur (Zahlenmauern berechnen und Auffälligkeiten beschreiben). Der Inhalt ist unterschiedlich. Der Anforderungsbereich der Aufgabe 1 liegt im Zahlenraum bis 20, der Anforderungsbereich der Aufgabe 2 im Zahlenraum bis 100.
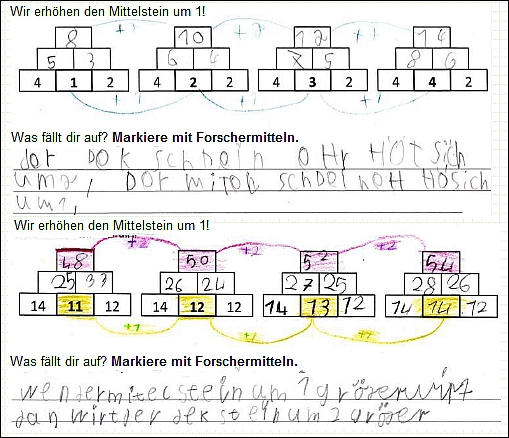 Aufgaben der gleichen Struktur, aber mit unterschiedlichen Inhalten bzw. Anforderungsbereichen
Aufgaben der gleichen Struktur, aber mit unterschiedlichen Inhalten bzw. Anforderungsbereichen
Tipps und Herausforderungen bereithalten
Die Tabelle zeigt einen Überblick über die verschiedenen Niveaustufen. Das zentrale Niveau umfasst eine Basisstufe mit einer Erweiterungs- bzw. Unterstützungsstufe. Darüber hinaus sind zur Förderung besonders leistungsstarker Schülerinnen und Schüler zusätzlich noch Erweiterungsstufen und zur Förderung von Kindern mit einem besonderen Unterstützungsbedarf zusätzliche Unterstützungsstufen vorgesehen. Jeder Niveaustufe sind entsprechende Anforderungen zugeordnet. Die Bearbeitung der Aufgabenstellung wird in den Unterstützungsstufen durch unterschiedliche Formen der individuell angepassten Lernunterstützung (Tipps, Hilfsaufgaben, Sternchenaufgaben, Transferaufgaben, …) erleichtert.
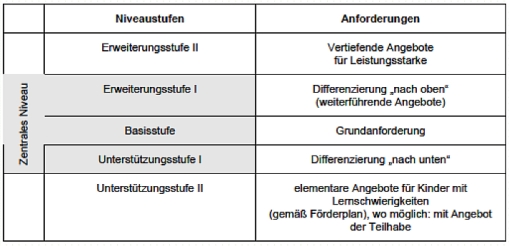
Übersicht über Niveaustufen und zugeordnete Anforderungen
Zur näheren Erläuterung ist im nachfolgenden eine Aufgabe zur Repräsentation der Basisstufe dargestellt. Ergänzend sind jeweils zudem eine Aufgabe zur Erweiterung und Unterstützung aufgezeigt.
Basis
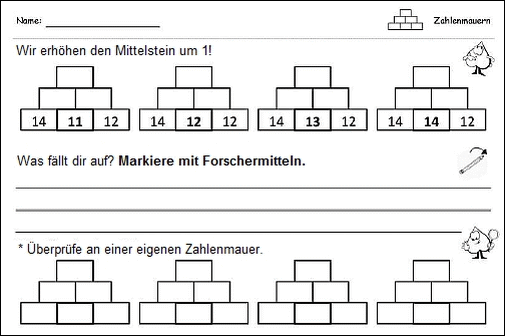
Aufgaben der Basisstufe
Unterstützung durch Verringerung des Zahlenraumes

Aufgaben der Unterstützungsstufe
Erweiterung durch Erhöhung des Mittelsteins um n
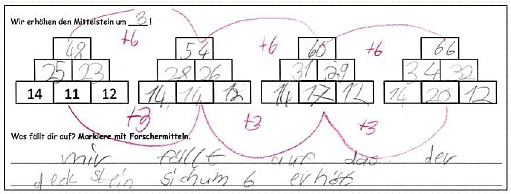
Aufgaben der Erweiterungsstufe
Offene Aufgaben einsetzen
Die Schülerinnen und Schüler wählen Aufgabenstellungen im Rahmen der zur Verfügung stehenden Varianten selbst aus. Komplexität und Anspruchsniveau können sie, ausgehend von ihren Lernmöglichkeiten, selbst bestimmen.
Das nachfolgende Beispiel zu Entdeckungen an der Hundertertafel zeigt, wie die Kinder selbst bestimmt Entdeckungen markieren bzw. im Forscherbericht näher erläutern. Durch die offene Aufgabenstellung ist eine natürliche Differenzierung gegeben.
 Selbstbestimmtes Lernen durch offene Aufgaben
Selbstbestimmtes Lernen durch offene Aufgaben



